
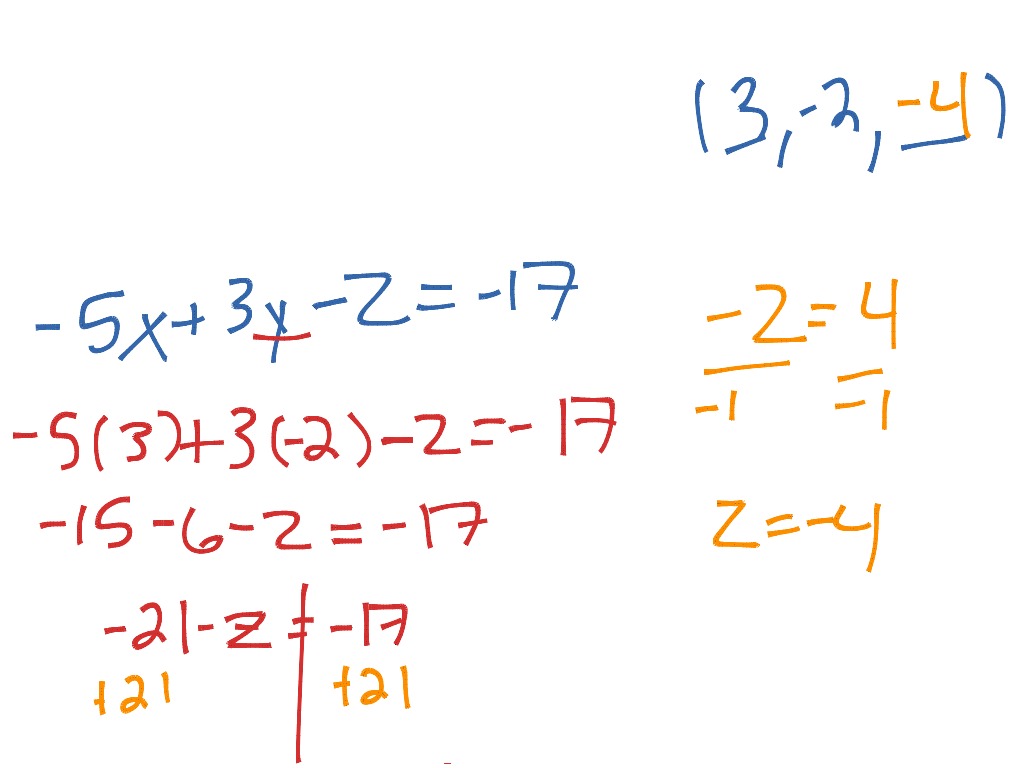
Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or two identical planes that intersect the third on a line.These systems are characterized in that all their equations share the same solution. After performing elimination operations, the result is an identity. Find the solution to a system of 3 equations in three variables. 3×3 systems of equations are systems of three equations with three variables. A system of equations in three variables is dependent if it has an infinite number of solutions.Systems of equations in three variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location.After performing elimination operations, the result is a contradiction. A system of equations in three variables is inconsistent if no solution exists.Systems of three equations in three variables are useful for solving many different types of real-world problems. Systems of linear equations can be used to solve resource allocation prob.The steps include interchanging the order of equations, multiplying both sides of an equation by a nonzero constant, and adding a nonzero multiple of one equation to another equation. To solve the system of equations, we can utilize functions and the equation solver tool.
3X3 EQUATION SYSTEMS SERIES
A system of three equations in three variables can be solved by using a series of steps that forces a variable to be eliminated. In mathematical terms, the system of equation is set of two or more equations having the same set of unknown variables like x, y, z where we need to find the values of unknown variables to solve these equations. Example Elimination method for 3x3 systems of equations elimination method for 3x3 systems of equations example let the system be: 15 20 10 step any two.
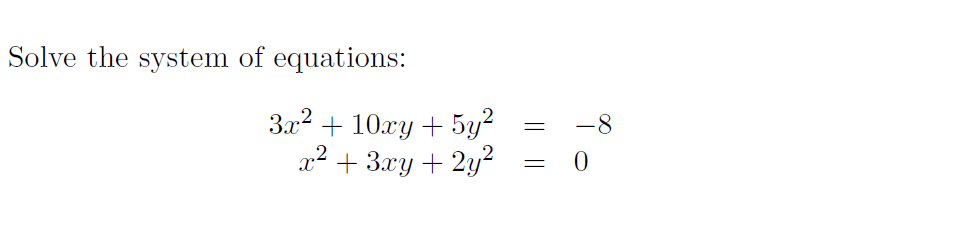
A solution to a system of three equations in three variables \left(x,y,z\right),\text that represents the intersection of three planes in space. In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. Solve Systems of Three Equations in Three Variables However, finding solutions to systems of three equations requires a bit more organization and a touch of visual gymnastics. Doing so uses similar techniques as those used to solve systems of two equations in two variables. We will solve this and similar problems involving three equations and three variables in this section. Understanding the correct approach to setting up problems such as this one makes finding a solution a matter of following a pattern.


 0 kommentar(er)
0 kommentar(er)
